Sigma-algebra

In mathematics, a σ-algebra (also sigma-algebra, σ-field, sigma-field or Borel-field) is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, a σ-algebra is the collection of sets over which a measure is defined. This concept is important in mathematical analysis as the foundation for Lebesgue integration, and in probability theory, where it is interpreted as the collection of events which can be assigned probabilities.

By definition, a σ-algebra over a set X is a nonempty collection Σ of subsets of X (including X itself) that is closed under complementation and countable unions of its members. It is a Boolean algebra, completed to include countably infinite operations. The pair (X, Σ) is also a field of sets, called a measurable space.

Thus, if X = {a, b, c, d}, one possible sigma algebra on X is

Σ = { ∅, {a, b}, {c, d}, {a, b, c, d} }.

Contents

Motivation

A measure on X is a function which assigns a real number to subsets of X; this can be thought of as making precise a notion of "size" or "volume" for sets. One would like to assign such a size to every subset of X, but in many natural settings, this is not possible. For example the axiom of choice implies that when the size under consideration is the standard notion of length for subsets of the real line, then there exist sets known as Vitali sets for which no size exists. For this reason, one considers instead a smaller collection of privileged subsets of X, which will be called the measurable sets, and which are closed under operations that one would expect for measurable sets, that is the complement of a measurable set is a measurable set and the countable union of measurable sets is a measurable set. Non-empty collections of sets with these properties are called σ-algebras.

Definition and properties

Let X be some set, and 2X its power set. Then a subset Σ ⊂ 2X is called σ-algebra if it satisfies the following three properties:

  1. Σ is non-empty: There is at least one A ⊂ X in Σ.
  2. Σ is closed under complementation: If A is in Σ, then so is its complement, X \ A.
  3. Σ is closed under countable unions: If A1, A2, A3, ... are in Σ, then so is A = A1 ∪ A2 ∪ A3 ∪ … .

From these axioms, it follows that the X itself and the empty set are both in Σ, because since by (1) Σ is non-empty, you can pick some A ⊂ X, and by (2) you know that X \ A is also in Σ. By (3) A ∪ (X \ A) = X is in Σ. And finally, since X is in Σ, you know by (2) that it's complement, the empty set is also in Σ.

It also follows that the σ-algebra is also closed under countable intersections (by applying De Morgan's laws). In fact, this is precisely the difference between a σ-algebra and a σ-ring: a σ-algebra Σ is just a σ-ring that contains the universal set X. At the same time a σ-ring need not be a σ-algebra, for example measurable subsets of finite Lebesgue measure in the real line are a σ-ring but not a σ-algebra.

Elements of the σ-algebra are called measurable sets. An ordered pair (X, Σ), where X is a set and Σ is a σ-algebra over X, is called a measurable space. A function between two measurable spaces is called measurable function if the preimage of every measurable set is measurable. The collection of measurable spaces forms a category, with the measurable functions as morphisms. Measures are defined as certain types of functions from a σ-algebra to [0, ∞].

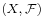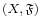σ-algebras are sometimes denoted using calligraphic capital letters, or the Fraktur typeface. Thus (X, Σ) may be denoted as \scriptstyle(X,\,\mathcal{F}) or \scriptstyle(X,\,\mathfrak{F}). This is handy to avoid situations where letter Σ may be confused for the summation operator.

Generated σ-algebra

Let F be an arbitrary family of subsets of X. Then there exists a unique smallest σ-algebra which contains every set in F (even though F may or may not itself be a σ-algebra). This σ-algebra is denoted σ(F) and called the σ-algebra generated by F.

To see that such a σ-algebra always exists, let 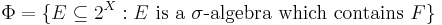\Phi=\{E\subseteq 2^X�: E\text{ is a }\sigma\text{-algebra which contains }F\}. The σ-algebra generated by F will therefore be the smallest element in Φ. Indeed, such a smallest element exists: First, Φ is not empty because the power set 2X is in Φ. Consequently, let σ* denote the (nonempty!) intersection of all elements in Φ. Because each element in Φ contains F, the intersection σ* will also contain F. Moreover, because each element in Φ is a σ-algebra, the intersection σ* will also be a σ algebra (observe that if every element in Φ has the three properties of a σ-algebra, then the intersection of Φ will as well). Hence, because σ* is a σ-algebra which contains F, σ* is in Φ, and because it is the intersection of all sets in Φ, σ* is indeed the smallest set in Φ by definition, which in turn implies that σ* = σ(F), the σ-algebra generated by F.

For a simple example, consider the set X = {1, 2, 3}. Then the σ-algebra generated by the single subset {1} is σ({1}) = {∅, {1}, {2,3}, {1,2,3}}. By an abuse of notation, when the collection of subsets contains only one member, call it A, one may write σ(A) instead of σ({A}).

Examples

Let X be any set, then the following are σ-algebras over X:

Examples for generated algebras

An important example is the Borel algebra over any topological space: the σ-algebra generated by the open sets (or, equivalently, by the closed sets). Note that this σ-algebra is not, in general, the whole power set. For a non-trivial example, see the Vitali set.

On the Euclidean space Rn, another σ-algebra is of importance: that of all Lebesgue measurable sets. This σ-algebra contains more sets than the Borel σ-algebra on Rn and is preferred in integration theory, as it gives a complete measure space.

See also

External links